サンプルコードのダウンロード
では、まずサンプルコードをダウンロードし、解凍してください。
私はVisual C++6.0でコンパイルしているので、お持ちの方はVisual C++でプロジェクトファイルを開いてください(「game_04.dsw」をダブルクリックすれば開けます)。
圧縮ファイルに含まれる「game_04.exe」をダブルクリックし、実行してみてください。
どうでしょう?画面が切り替わり、フルスクリーン化すると思います。
そして、カーソルの左右で角度を変更でき、上でその角度の方向へキャラクタが移動すると思います。
三角関数のお勉強 ステップ1
さて、三角関数とはなんぞや?という人のためにササっと解説してしまいます。
(高校2までに習うとは思いますが・・・)
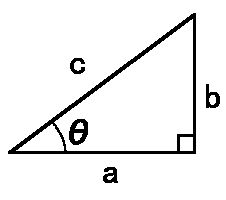
左の図形を見てください。こういった直角三角形がある場合、
① sinΘ=b/c
② cosΘ=a/c
③ tanΘ=b/a
といった定義が存在します。ちなみに、①から順番に、サイン・コサイン・タンジェントと読みます。
ここでよくある(?)問題
A君は、とある木から10m離れた所で、地面に突っ伏し、そこから
丁度45度の角度でその木の一番高い所を見ていました。
さて、この木の高さは何mでしょう。
まぁ、この場合↑の図形で言う所のbが高さ、aが10m(木とA君の距離)ですね。
で、bを求めたくて、解っているのがaと45度という角度なので③の「tanΘ=b/a」を使って解いてやればいいですね?
tan45°=b/10
b=tan45°×10
b=1×10
答え 10m
となります。
まぁ「tan45°」のように
解りやすい角度なら頭の中でも計算できますが「tan2°」だと、直ぐ答えれる人はなかなかいないでしょう(たぶん。
幸い、C言語にはあらかじめ、sin,cos,tanの関数が用意されているので、値を簡単に出せます。
三角関数のお勉強 ステップ2
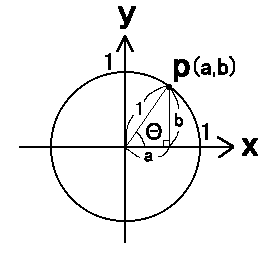
さて、基本が解ったところで(?)左のような半径1の円上にある点Pの座標(a,b)を表わすにはどうすればいいでしょう(かなり強引)。
こいつらも三角関数を使用してやります。
まず、点pのX座標がa、原点から点pまでの長さが1(半径1より)という事で
cosΘ=a/1
a=cosΘ
となります。
同様に、点pのY座標がb、原点から点pまでの長さが1という事で
sinΘ=b/1
b=sinΘ
となります。よって、半径1の円上にある点Pの座標はP(cosΘ、sinΘ)と表わす事が出来るわけです。
三角関数のお勉強 ステップ3
さて、ここで問題(またかよー)。点P(cx,cy)がΘ°の方向へ1進んだ時の座標はどう表されるでしょう?
もうお分かりですね?半径1の円上にある点Pの座標はP(cosΘ、sinΘ)という事から、
P( cx+cosΘ , cy+sinΘ )
となりますね。また、進みたい距離が1ではなく t だとしたら
P( cx+cosΘ×t , cy+sinΘ×t )
という事になります。
C言語で三角関数を使用する方法
ここまでで、三角関数の基本はバッチリ身に付いたと思います(そんなことないってか?)。
C言語で三角関数を使用するには、まず「math.h」をインクルードしてやります(まぁ当たり前ですね)。
それでは「三角関数のお勉強ステップ3」をそのままC言語で表してみましょうか。
キャラクターの座標が cx , cy の時、 angle 度の方向へ t 進みたい場合、
cx+=cos(angle)*t; cy+=sin(angle)*t;
と、なるはずですが、パソコンのディスプレイ上の y 座標は、下に行く程増加していく、つまり数学上の座標とはy軸の向きが反対になります。
ですから、
cx+=cos(angle)*t; cy-=sin(angle)*t;
でOK・・・となるはずですが、まだです(爆
C言語の cos , sin 等の引数はラジアンという単位で指定しなければなりません。
まぁラジアンについては私もよく知らないので数学の先生に聞いてください。
とにかく180°はラジアンでπと表わされるので、
1°はπ/180ですよね?
よって
cx+=cos(angle*3.1415926535/180)*t; cy-=sin(angle*3.1415926535/180)*t;
これで、一応動作します。
ちょっとした高速化のお話
さて、C言語で毎回 cos() , sin() とかを呼び出してごちゃごちゃ計算させるのは処理の無駄であり、
ゲームの速度を落とす原因となりかねません。
ですから、ちょっと工夫して高速化させてやります。
と言っても、ただあらかじめテーブル作成しておくだけなんですけどね。
//サイン、コサインテーブル作成
float fsin[360],fcos[360];
int i;
for(i=0;i<360;i++){
fsin[i]=(float)sin(i*3.1415926535/180);
fcos[i]=(float)cos(i*3.1415926535/180);
}
こいつらを作成してやれば
cx+=cos(angle*3.1415926535/180)*t; cy-=sin(angle*3.1415926535/180)*t;
が
cx+=fcos[angle]*t; cy-=fsin[angle]*t;
で済みます。
ただ、角度angleは0~359の範囲でないといけないし、
0.5といった少数で指定する事も出来なくなります。
ですが、シューティングゲームのように、速度重視且つ、 sin , cos で精度にあまりとらわれなくても良いような場合はテーブルでやった方が良いですね。
サンプルコードの解説
では、サンプルコードを見てみましょう。
int PASCAL WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpszCmdParam, int nCmdShow){
<略>
// cx:座標 cy:座標 mv:移動量
float cx=320.0f-16,cy=240.0f-16,mv=3.0f;
// angle:向いている角度
int angle=0;
//サイン、コサインテーブル作成
float fsin[360],fcos[360];
int i;
for(i=0;i<360;i++){
fsin[i]=(float)sin(i*3.1415926535/180);
fcos[i]=(float)cos(i*3.1415926535/180);
}
//メインループ
while(1){
WaitSet(); //現在の時間(単位:ミリ秒)取得
ClearScreen(lpBack); //バックバッファ初期化
DdTextOut(lpBack,0,0,"←、→で旋回 ↑で進む pauseキーで終了",255);
sprintf(tmp,"現在向いている角度 %d",angle);
DdTextOut(lpBack,0,16,tmp,255);
//旋回
if(keyg[37]){ //←
angle+=5;
//cos,sinは配列を使用しているので角度が0~359になるように調整する必要がある
if(angle>=360)
angle-=360;
//angle%=360;と書ける
}
if(keyg[39]){ //→
angle-=5;
if(angle<0)
angle+=360;
//angle=(angle+360)%360;と書ける(たぶん
}
//向いている角度へ進む
if(keyg[38]){ //↑
cx+=fcos[angle]*mv;
cy-=fsin[angle]*mv;
}
//キャラクタ表示
BltClip(lpBack,(int)cx,(int)cy,32,32,lpWork,0,0,1);
Flip(); //フィリップ
Wait(1000/60); //メッセージループへ
}
キャラクタの座標(cx,cy)はfloat型で宣言します
(「int a=0; a+=0.5」とやってもaの値は0のままというのは当たり前ですからね)。
んー、まぁ後は大体上の方で説明したので解ります。








